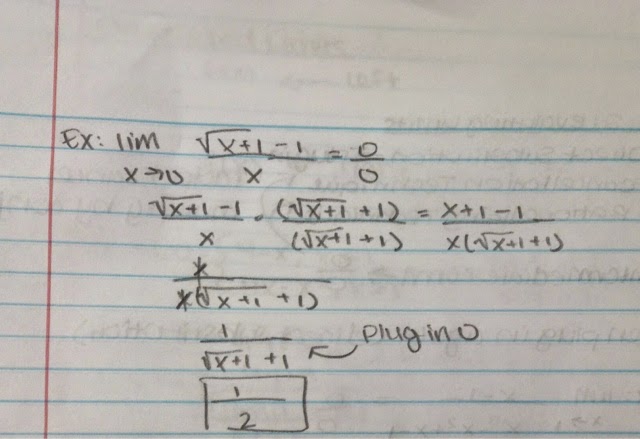12.2: Evaluating Limits

There are three main ways to evaluate limits.

1) direct substitution (plug-in) 

2) cancellation technique (factor and cancel) 

3) rationalizing technique (multiply by the conjugate-only used with problems with radicals) 

You should use the direct substitution first. If using direct substitution gives you 0/0, then it is in intermediate form. If it is in intermediate form, then you have to either use the cancellation technique or the rationalizing technique to get a new equation. Then plug the number from the original equation into the new equation. 

Example of the cancellation technique

 

Example of the rationalizing technique

One-sided limits

Sometimes there are problems like this:

In these types of problems, you have to plug it in to both eqautions. If it the result is the same for each equation then there is a limit. In this case, the limit is 3. If the result for each eqaution is different, then it is a one sided equation and you can solve for each side separately. 

In other cases, the problem has a f(x) in it and you have to first solve the function before solving the main equation to find the limit. 

Math joke of the day:

Interesting Math Stuff #13: John Nash

John Forbes Nash is a modern mathematician who made considerable advances in many contributions to the fields of game theory, differential geometry, no partial differential eqautions. 

One of his most interesting contributions was involved encryption which we studied earlier this year. In 2011, the NSA revealed some of Nash's letters where he discussed a new encryption/decryption machine. 

Nash was also diagnosed with paranoia and schizophrenia which caused his hospitalization. His mathematical genius and his mental disorders inspired a 2001 Hollywood film named A Beautiful Mind. 

Math joke of the day:

11.2: 3-D Vectors

Component form: v=<v1, v2, v3>

Unit vector form: v=v1i+v2j+v3k

Length formula: 

Length can also be called tension or magnitude. 

Unit Vector:

Vector addition and dot product:

Angle between two vectors formula:

Orthogonal if...

-The dot product between the two vectors is 0

-The angle between the vectors is 90 degrees

Parallel if...

u=cv

Vector 1=(constant)(vector 2) 

-the points are collinear 

Math joke of the day:

11.1: 3-D graphs introductions

Today we learned about 3-D graphs. 

With the points (x1, y1, z1) and (x2, y2, z2) 

The distance and midpoint formula:

The eqaution of a sphere:

r=radius

center=(h, k, j) 

Math joke of the day:

3-D Graphs

Check out these cool 3-D graphs I made on the apps quick graph and good graph!